1.什么是递归?

递归是一种在程序设计语言中广泛应用算法。一种编程思想和技巧。 其主要特点就是通过反复调用自身函数来解决问题。
举个例子来说：
黑蓝白红
有一天黑兔想吃蓝萝卜，但他只有黑萝卜，于是他去找蓝兔，
蓝兔说，我想吃白萝卜，找到了我就把我手上的蓝萝卜给你。于是他去找白兔；
白兔说，我想吃红萝卜，找到了我就把我手上的白萝卜给你。于是他去找红兔；
红兔说，我想吃黑萝卜，找到了我就把我手上的蓝萝卜给你。

黑兔想，我不是正好有黑萝卜吗？

于是黑兔把黑萝卜给他，换到了红萝卜。
用红萝卜换到白兔的白萝卜；
用白萝卜换到蓝兔的蓝萝卜；
最后黑兔得到了自己想要的蓝萝卜。

这个故事中：
黑兔找萝卜的过程就是递，
萝卜换萝卜的过程就叫归。
黑兔有黑萝卜就是这个问题最核心的点，也就是递的终止点。

把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解
递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算，减少了程序的代码量。

2.主要思想

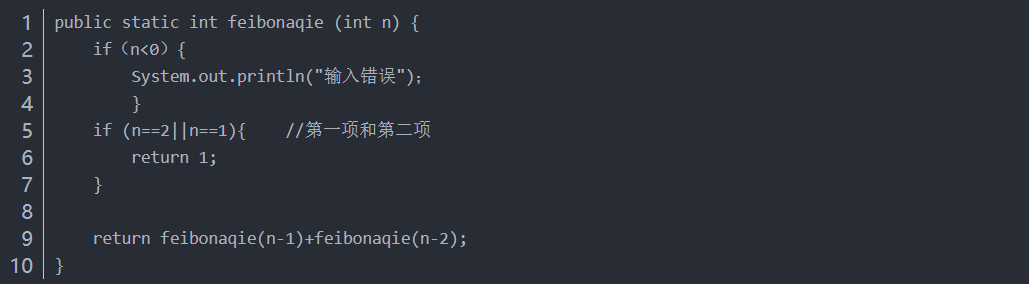
一般会用斐波那契数列来讲解递归思想。
第1.2项为1，以后的每一项都为 前两项之和：
1，1，2，3，5，8，13…
会让求第n项斐波那契数，
如何的到第n项呢？要是知道第n-1项和n-2就好了；
如何的到第n-1项呢？要是知道第n-2项和n-3就好；
…
如何的到第3项呢？要是知道第2项和1就好；

第2项和第1项我们知道啊（喏，我手上的黑萝卜给你！）

然后我们可以的到第3项，第4项…最后的到第n项

3.递归编程

递归和循环很类似，及重复运行某一段代码，
一般来说，递归需要有边界条件、递归前进段和递归返回段。

用汉诺塔的例子可以更好的理解递归思想
有A,B,C三个竖杆，A上有上从下往上按照大小顺序摞着n个圆盘。将A上的圆盘按同样规则移动到C上，一次只能移动一个原配。求需要多少步，怎么移动？
这个问题咋一看特别复杂，用循环更是摸不着头脑。看看用递归是怎么解决的。

按递归的思想，要将n个A上的圆盘移动到C上，我们需要知道n-1个圆盘时是怎么移动.

知道后我们可以将n-1个圆盘先移动到B上，然后将A上最底下一个移动到C上，然后再用n-1个时方法将B上的n-1个圆盘移动到C上
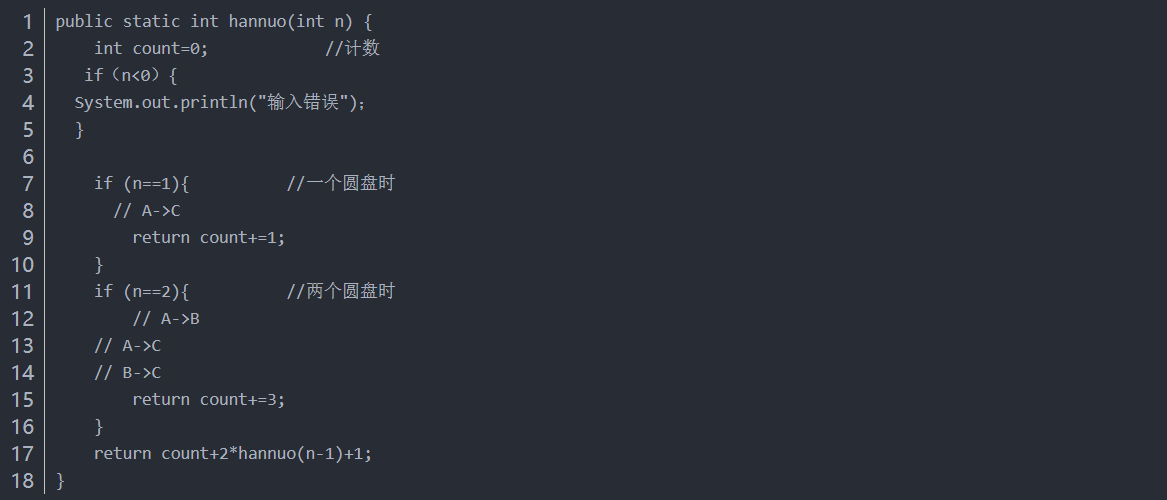
可以的出第n项和n-1项的关系为f（n）=2*f（n-1）+1

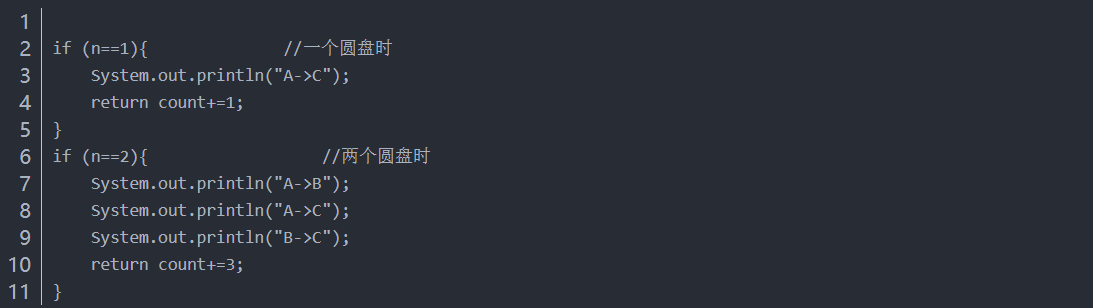
最终就是我们只需要知道1个和2个圆盘时是怎么移动的，我们就解决这个问题。

然后加上前推条件

完整的程序就能得到了

递归思想编程时最明显的特点就是代码少，且简单，同时它的缺点也暴露出来，占内存较大，计算速度慢。